[JAVA] 다이나믹 프로그래밍(Dynamic Programming)

한 번 계산한 문제는 다시 계산하지 않도록 하는 알고리즘

---

다이나믹 프로그래밍(Dynamic Programming)

최적의 해를 구하기에 시간이 매우 많이 필요하거나 메모리 공간이 매우 많이 필요한 문제 등,

컴퓨터로도 해결하기 어려운 문제가 있습니다.

다이나믹 프로그래밍은 메모리 공간을 약간 더 사용하며

연산 속도를 비약적으로 증가시킬 수 있는 방법으로, 동적 계획법이라고도 표현합니다.

 

다이나믹 프로그래밍에는 두가지 방식(탑다운, 보텀업)이 있습니다.

다이나믹 프로그래밍을 위해 자주 사용되는 메모이제이션 기법도 알아보겠습니다.

 

다이나믹 프로그래밍으로 해결할 수 있는 대표적인 예시로 피보나치 수열이 있습니다.

피보나치 수열은 이전 두 항의 합을 현재의 항으로 설정하는 특징이 있는 수열입니다.

 

1   1   2   3   5   8   13   21   34   55   89   ...

이 수열은 a(n) = a(n-1)+a(n-2), a1= 1, a2= 2 이렇게 정의 할 수 있습니다.

 

피보나치 수열을 재귀함수로도 정의할 수 있습니다.

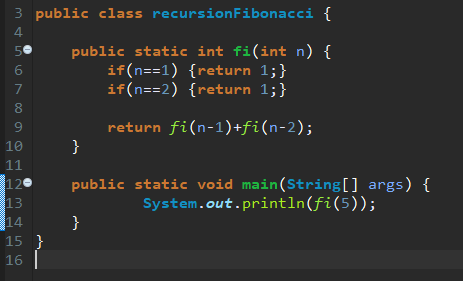
public class recursionFibonacci {

	public static int fi(int n) {
		if(n==1) {return 1;}
		if(n==2) {return 1;}
		
		return fi(n-1)+fi(n-2);
	}
	
	public static void main(String[] args) {
			System.out.println(fi(5));
	}
}

그러나 이렇게 작성하게 되면 fi 메소드에서 n이 커지면 커질수록

동일한 함수가 반복적으로 호출되기 때문에 수행 시간이 기하급수적으로 늘어납니다.

 

다이나믹 프로그래밍을 사용하면 효율적으로 해결할 수 있습니다.

하지만 항상 다이나믹 프로그래밍을 사용할 수 없으며 다음 조건을 만족할 때만 사용할 수 있습니다.

 

조건1 ) 큰 문제를 작은 문제로 나눌 수 있다.

조건2 ) 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

 

메모이제이션(Memoization) 기법은 다이나믹 프로그래밍을 구현하는 방법으로 ,

한번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하는 기법입니다.

 

메모이제이션 기법을 사용하게 되면 5번째 피보나치 수를 호출할 때에는 다음 그림처럼 색칠한 노드만

방문하게 됩니다.

 

다이나믹프로그래밍을 적용했을 때의 피보나치 수열 알고리즘의 시간복잡도는 O(N)입니다.

 

 

다이나믹 프로그래밍을 이용한 소스코드

- 재귀함수를 이용한 탑다운(Top-Down, 하향식)방식

package dynamicProgramming;

public class TopDown_Fibonacci {
	public static int[] arr;
	public static int fi(int n) {
		if(n==1) {return 1;}
		if(n==2) {return 1;}
		
		if(arr[n]!=0) {return arr[n];}
		
		return fi(n-1)+fi(n-2);
	}
	
	public static void main(String[] args) {
			int n =6;
			arr= new int[n+1];
			System.out.println(fi(n));
	}
}



결과 : 8

 

- 반복문을 이용한 보텀업(Bottom-Up, 상향식)방식

package dynamicProgramming;

public class BottomUp_Fibonacci {
	public static int[] arr;
	public static int fi(int n) {
		arr[1]=1;
		arr[2]=1;
		for (int i = 3; i <= n; i++) {
			arr[i]=arr[i-1]+arr[i-2];
		}
		return arr[n];
	}
	
	public static void main(String[] args) {
			int n =6;
			arr= new int[n+1];
			System.out.println(fi(n));
	}
}


결과 : 8